＜解答編＞助言と、悪手と、モンティ・ホール問題と、ロシアンルーレット

「２分の１」じゃないの？

プロ棋士の助言後、残る選択肢は２つ、正解は１つ。確率は２分の１にみえる。しかし違う。あなたは、下記情報を知っている。

プロ棋士は、あなたが選んだ手「A」を見て、それ以外の手（「B」、「C」）の中から悪手を１手教えてくれた。

これが大きくものをいう。プロ棋士は、仮に「A」と「B」が悪手だったとしても、「A」とは助言できない状況にあった（「B」と助言するしかない）。「A」と「C」が悪手だったとしても同様に、「C」と助言するしかない。

プロ棋士が、「C悪手」と助言をした経路

プロ棋士が「C悪手」と助言をするには、２通りの経路がある。すなわち、

1. 正解手が「A」（手を変えなければ正解！）で、プロ棋士が「C悪手」と助言
2. 正解手が「B」（手を変えれば正解！）で、プロ棋士が「C悪手」と助言

どちらの経緯で「C悪手」、と助言するにいたったか。確実にはわかるわけがない（それすなわちあなたが最善手をわかることになってしまう）。しかし、どちらの経緯で「C悪手」、と助言した確率が高いかは、計算することができる。下記の表を見てみよう。

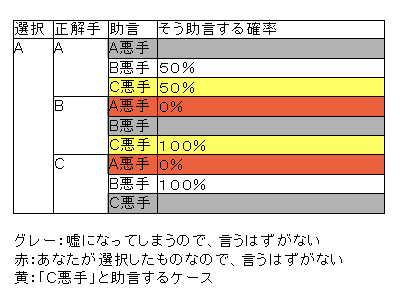
• １．の経路、すなわち正解手が「A」の場合
  • 「B悪手」と助言する確率と「C悪手」と助言する確率は50％と等しい。その確率を経て、「C悪手」、と助言したことになる。
• ２．の経路、すなわち正解手が「B」の場合
  • 「A悪手」、「B悪手」とは助言できないので、必ず「C悪手」と助言する。

したがって、２．の経路、すなわち正解手が「B」の場合の経路を通って、「C」は悪手と助言した確率のほうが２倍高い。よって、手を変えたほうが正解に近づく。
参考までに、選択肢を５手に増やし、あなたが「A」を選択、プロ棋士がそれ以外の「B」〜「E」のうち、「B」以外（すなわち「C」「D」「E」）を「悪手」と助言してくれた場合の表を下記に示しておく。手を「A」から「B」に変えると４倍当たる確率が高くなることがわかるだろう。

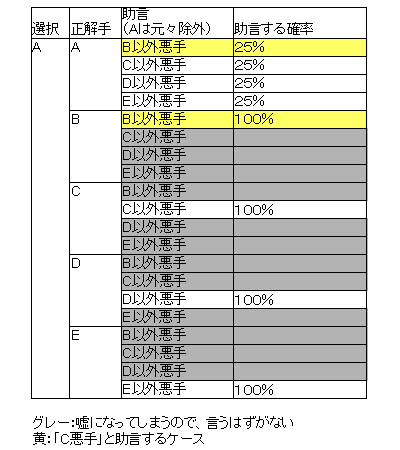
実践的解説としては、「DOFI-BLOG どふぃぶろぐ ネコでもわかるモンティホールジレンマ」がFlashを使ってわかりやすく作られている。参考になるだろう。が、数学的解説としては不十分（というか誤り？）。なぜ問題２のケースの解答が異なるのか、解説できないのではないだろうか。

ポイントは、プロ棋士はあなたが選んだ手を絶対に選ばないので、必ずゲームは成立する、ということ。問題２の場合は異なる。

プロ棋士が、「C悪手」と助言をした経路

問題１と同じく、経路は２つ。

1. 正解手が「A」で、プロ棋士が「C悪手」と助言（手を変えなければ正解！）
2. 正解手が「B」で、プロ棋士が「C悪手」と助言（手を変えれば正解！）

ただし、表にするとその中身の違いがわかる。

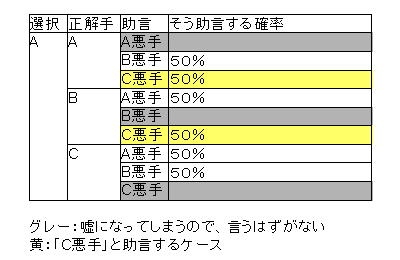
• １．の経路、すなわち正解手が「A」の場合
  • 「B悪手」と助言する確率と「C悪手」と助言する確率は50％と等しい。その確率を経て、「C悪手」、と助言したことになる。
• ２．の経路、すなわち正解手が「B」の場合
  • 「A悪手」と助言する確率と「C悪手」と助言する確率は50％と等しい。その確率を経て、「C悪手」、と助言したことになる。「A悪手」と助言する可能性もあった、というのがポイント。

したがって、どちらの経路を通ってきたかは等しく、1/2の確率である。よって、当たる確率も1/2。

ここで１つポイントなのが、「A悪手」と助言してくれた場合。「A」選択の場合は喜び勇んで手を変えるわけだが、結局残る「B」「C」の当たる確率はそれぞれ1/2。どう助言をつぶやいてくれようが、残る２手の当たる確率は1/2なのだ。「A」中心で進めていた自分の読み筋が却下されたわけで、このときのほうが物理的（読んだ手数の数）にも精神的にも痛いだろう。なお本ゲームにおいては、はじめに「A悪手」と助言していたら、その時点でルールに逸脱することになり、ゲームはやり直しとなる。ちなみにこれは1/3の確率。３回に１回はゲームやり直し、ということだ。

できればこの例を実践するFlashを作りたいものだが、時間がかかりそうなのでやめておく。（上のFlash作っている方、作っていただけないかな）